Connect four principiae
Vier gewinnt ist ein simples Brettspiel, bei dem zwei Spieler vier Steine in eine Reihe bekommen müssen -- ähnlich wie bei Tic-Tac-Toe. Aber:
- Vier gewinnt spielt man auf einem 7 x 6 großen Brett (Tic-Tac-Toe: 3 x 3)
- Bei Vier gewinnt 'fallen' die Steine auf unbesetzte Felder (bei Tic-Tac-Toe kann man seine Steine auf jedes freie Feld setzen)
- Bei Vier gewinnt muss man vier Steine in eine Reihe bekommen (bei Tic-Tac-Toe nur drei Steine)
Die genauen Regeln stehen in der Wikipedia:
"Computerisierung" bedeutet hier nicht nur, dass ein Programm das Brett aufzeichnet und die Spielregeln verkörpert, sondern auch, dass es einen interessanten Gegner bietet. Dieser Wiki-Artikel erklärt eine simple Methode zur Konstruktion eines solchen Computerprogramms. Achtung: Vier gewinnt ist ein gelöstes Spiel, d.h. es gibt Programme, die immer gewinnen, weil sie alles über das Spiel wissen und einen Sieg vom ersten Zug weg erzwingen können. (Zieht der Mensch zuerst, kann der Computer ein Unentschieden erzwingen.) Die hier erklärte Methode ist keine solche Ausführung, liefert aber gute Resultate -- sogar auf kleinen (= 8-bit) Computern.
Gewinnen = finden
Vier gewinnt ist ein Strategiespiel. Um zu gewinnen, muss man
- die möglichen zukünftigen Züge im Geist durchgehen
- dann überlegen welche Konsequenzen die einzelnen Züge haben, d.h. weiter in die Zukunft denken
- einen Zug wählen, der für die Zukunft strategische Vorteile schafft, d.h. unter den möglichen Zügen den vorteilhaftesten auswählen
Da das Vier gewinnt-Brett ("grid") sieben Spalten ("columns") zum Einwerfen hat, stehen beide Spieler für jeden Zug ("ply") vor (höchstens) sieben Möglichkeiten:

Ein Spieler, der im Geiste die Konsequenzen für seinen Zug überdenken will, muss von der neuen Situation weg für seinen Gegner ziehen. So entsteht ein buschiger Baum mit sieben Ästen, die ihrerseits sieben Äste haben. So muss der Spieler nach zwei Zügen 49 verschiedene Bretter bewerten:
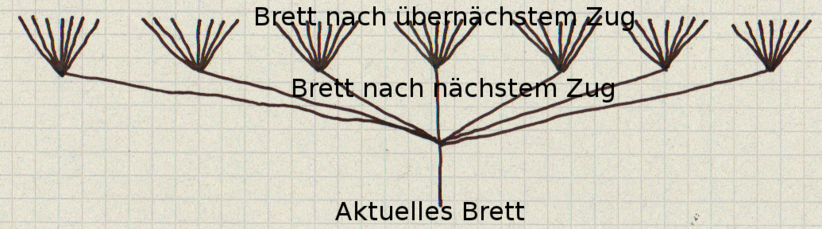
Um so mehr Züge man in die Zukunft blickt, um so "tiefer" man über eine gegebene Situation am Brett nachdenkt, um so mehr Bretter muss man bewerten:
- 1 Zug: 7 Bretter
- 2 Züge: 49 Bretter
- 3 Züge: 243 Bretter
- 4 Züge: 2401 Bretter
Ein Computerprogramm kann gewinnen, wenn es den Baum der möglichen Zukünfte absucht und eine siegreiche Spielsituation entdeckt. Hier ist ein Baum mit nur zwei Möglichkeiten pro Zug. Das vereinfacht die Darstellung.
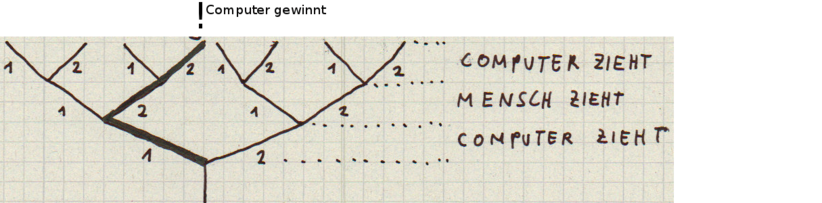
Da der Computer einen Sieg im Zweig 1-2-2 entdeckt, liegt es nahe, sich für den Zug 1 zu entscheiden, denn der führt zum Sieg. Die Sache hat einen Haken: im Geist des Gegners laufen ganz ähnliche Denkprozesse ab. Der Gegner will einen von siegreichen Abzweigungen weg bringen. Betrachten wir diesen Baum:
FIXME
Hier könnte der Computer durch Wahl von 1 zwar auch gewinnen, aber sein Gegner lässt ihn natürlich nicht. Sein Gegner vereitelt nach Zug 1 das Manöver und gewinnt selber mit seinem Zug 1. Die Suche im Baum muss widerspiegeln, dass der Gegner ebenfalls denken kann und eigene Ziele anstrebt. Dazu legen wir folgendes fest.
- Ein Brett mit einem Wert von 1 bedeutet: Computer gewinnt
- Ein Brett mit einem Wert von -1 bedeutet: Computer gewinnt
- Ein Brett mit einem Wert von 0 bedeutet: nichts besonderes (und wenn das Brett voll mit Steinen ist, dann ist das Spiel unentschieden)
Im Baum sucht der Computer in "seinen" Zweigen, d.h. jenen Zweigen, die seine eigenen Züge bedeuten, nach einem möglichst hohen Wert (d.h 1). In den Zweigen für die menschlichen Züge sucht der Computer nach einem möglichst geringen Wert (d.h. -1). Nach dieser Einsicht kann der Computer das Debakel aus dem vorigen Beispiel verhindern. Die Methode der Minimierung für den Menschen sondert Zug 1 aus und der Computer geht nicht in die Falle. Dieses Verfahren ("MinMax" für "Maximize-Minimize") wird im Abschnitt FIXME noch genauer erklärt.
Brettwerte von -1 für Verlieren, 1 für Sieg und 0 für nichts besonderes haben aber einen gewaltigen Nachteil: die allermeisten Züge, besonders am Anfang, liefern Bretter mit einem Wert von 0. Für den Computer sind sie daher alle gleich, d.h. er kann unter vielen scheinbar gleichen Zügen bloß irgendeinen wählen. Hier sind einige Bretter, die alle 0 liefern, aber sind sie alle gleichwertig?
FIXME
Die Antwort ist Nein. Betrachten wir die Bretter im eEinzelnen.
Das erste Brett (Abb. FIXME) zeigt ein noch nicht sehr fortgeschrittenes Spiel. "O" könnte zwar auf seinen kleinen Turm aus zwei "O"s noch zwei weitere draufsetzen um zu gewinnen, aber dieser Sieg liegt noch in der eher entfernteren Zukunft, besonders, wenn man bedenkt, dass "X" dieses Vorhaben leicht vereiteln kann.
Brett zwei ist schon weiter fortgeschritten. "X" kann zwar den vierten Stein zum Abschluss der diagonalen Kolonne noch nicht an seine Stelle setzen, weil dafür die Unterlage fehlt, aber die Gefahr für "O" ist bereits sehr deutlich und erfordert besondere Vorsicht:
Beim Vergleich der beiden Bretter sollte klar sein, dass Brett A für "O" weniger wert ist als Brett B für "X". Anders gesagt: Brett B sieht eher nach Sieg für "X" aus als Brett A für "O".
Noch extremer ist Brett C. Hier ist "X" am Zug, aber "O" hat bereits so gut wie gewonnen, denn pariert "X" die 3er-Kolonne links, dann zieht "O" auf die rechte Seite und gewinnt; falls "X" das rechte Feld besetzt, dann gewinnt "O" links. Dieses Brett hat einen sehr hohen Wert für "O", d.h. einen sehr negativen für "X":
In Brett D steht kein unausweichlicher Sieg unmittelbar bevor, aber auch dieses Brett hat einen ausgeprägteren Wert als A oder B. "X" hat ein dichtes Netz aus Gelegenheiten gewoben. Es gibt so viele fast fertige Kolonnen und Zwickmühlen für "O", dass "X" hier einen Sieg erzwingen kann. (Sogar, wenn wir annehmen, dass "O" am Zug ist.) Hier noch einmal Brett D:
Wie lassen sich diese Beobachtungen beziffern? Wie kommen wir zu einem numerischen Wert zu einer gegebenen Situation am Brett? Die Antwort dreht sich um die Einsicht, dass es nur eine sehr begrenzte Anzahl von Vierer-Kolonnen ("packs") im Raster gibt, auf denen man gewinnen kann. Besonders wenige solcher Packs gibt es bei einem ähnlichen Spiel, Tic-Tac-Toe. Tic-Tac-Toe hat neun Felder und acht Packs. Hier sind die Felder eines Tic-Tac-Toe-Bretts nummeriert:
Die acht Packs verlaufen horizontal (3 Stück), vertikal (3 Stück) und diagonal (3 Stück):
So lässt sich eine Tabelle mit den einzelnen Feldnummern für die jeweiligen Packs erzeugen:
0 1 2 3 4 5 6 7 8 0 3 6 1 4 7 2 5 8 0 4 8 2 4 6
Die entsprechende Tabelle für Vier Gewinnt umfasst 69 Packs. Ein Vier Gewinnt-Raster hat 42 Felder, nummeriert von 0 bis 41:
Pro Zeile (row) und Spalte (column) gibt es mehrere horizontale und vertikale Packs. Hier die vier horizontalen Packs in der ersten Zeile:
Dazu die ersten Einträge der Tabelle:
FIXME
Hier einige Beispiele für weitere Packs und die Felder, aus denen sie sich zusammensetzen:
Pack 0 (erstes):
Pack 8:
Pack 34:
Pack 50:
Pack 68 (letztes):
Um den Wert eines gegebenen Brettes zu ermitteln, macht der statische Evaluator folgendes:
- er klappert die Liste mit den 69 Packs ab, holt für jedes einzelne die vier Feldnummern
- er bewertet die Steine im Pack (dazu gleich mehr)
- er addiert die Werte der einzelnen Packs, um den Gesamtwert für das Brett zu erhalten
Wieviel ist ein Pack wert? Das hängt davon ab, wie weit es davon entfernt ist, durch vier gleiche Steine zu einem Sieg zu führen.
Ein leeres Pack - "leer-leer-leer-leer" - hat einen Wert von 0. Es ist von einem Sieg durch "X" und einem Sieg durch "O" gleich weit entfernt, hat aber aus Mangel an Steinen keinen Wert.
Ein Pack mit "leer-X-leer-leer" rückt in diesem Pack einen Sieg von "X" schon zart in die Nähe. Es hat daher einen geringen Wert für "X". Spielt der Computer "X", so muss er dem "leer-X-leer-leer"-Pack einen geringen postiven Wert geben.
Ein Pack mit "O-O-O-O" hat bringt nach dieser Logik dem Menschen ("O") den Sieg und hat daher (für den Computer) einen gigantischen negativen Wert.
Ein Pack mit "O-X-leer-leer" hat keinen Wert, denn hier kann weder "X" noch "O" gewinnen, denn dafür ist im Vierer-Pack kein Platz mehr.
Ein Pack mit "O-O-O-leer" macht den Sieg für den Menschen greifbar und hat daher bedeutenden negativen Wert.
Ein Pack mit "X-leer-X-X" macht den Sieg für den Computer greifbar und daher einen bedeutenden positiven Wert.
Diese Erkenntnis drücken wir aus, indem wir den Pack-Wert mit der Anzahl der "X" oder "O" exponentiell wachsen lassen, vorausgesetzt, dass im Pack nur gleiche Steine und ansonsten leere Felder sind. Daher:
- leere Packs: Wert 0
- nicht leere, aber mit unterschiedlichen Steinen besetzte Felder: Wert 0 (denn hier kann keiner der beiden mehr was gewinnen)
Ansonsten:
- 1 "O": -1
- 2 "O"s: -1 x 4 = -4
- 3 "O"s: -1 x 4 x 4 = -16
- 4 "O"s: -1 x 4 x 4 x 4 = -64 (Sieg für "O", muss gesondert behandelt werden, siehe FIXME)
- 1 "X": 1
- 2 "X"s: 1 x 4 = 4
- 3 "X"s: 1 x 4 x 4 = 16
- 4 "X"s: 1 x 4 x 4 x 4 = 64 (Sieg für "X", muss gesondert behandelt werden, siehe FIXME)
Die Basis (Faktor) 4 ist willkürlich gewählt und innerhalb gewisser Grenzen egal. Wichtig ist nur, dass ein Pack mit zwei gleichen Steinen einen DEUTLICH ausgeprägteren Wert hat als eines mit einem Stein, und eines mit drei gleichen Steinen einen deutlich ausgeprägteren als eines mit zwei gleichen.
Zur Veranschaulichung der Pack-Bewertung im Zusammenspiel ein Beispiel. Hier ist die Spielsituation:
Der Computer muss die Werte aller 69 Packs ins Kalkül ziehen, aber wir greifen hier nur drei heraus: 13, 41 und 54:
Sobald das Vier Gewinnt-Programm beim Abarbeiten der Pack-Liste bei 13 ankommt, holt es aus der Liste die entsprechenden Feld-Nummern (field numbers) -- 22, 23, 24 und 25. Nach Abbildung FIXME sind die Felder so besetzt: leer-leer-O-leer. Für Pack 13 erhalten wir daher den Wert -1 (siehe Tabelle Fixme).
Das nächste Pack, das wir untersuchen, ist 41, d.h. die Felder 17, 24, 31 und 38. Die entsprechenden Feldinhalte: leer-O-X-O. Da hier keiner mehr was gewinnen kann, hat das Pack den Wert 0.
Das letzte Pack in diesem Gedankenexperiment ist, d.h. die Felder 15, 23, 31 und 39. Feldinhalte: leer-leer-X-X. Wert: 16.
Die Werte -1, 0 und 16 müssen - zusammen mit den Werten der restlichen Packs im Brett - addiert werden, um den Gesamtwert des Brettes zu erhalten. In unserem Beispiel sind erst wenige Steine am Brett, daher sind die meisten Packs leer. (Eine bedeutende Verbesserung dieses Verfahrens ist: nur jene Packs zu bewerten, die vom gerade gesetzten Stein berührt werden, denn nur dort ändern sich die Pack-Werte. Diese Verbesserung wird in FIXME besprochen.)
Nach dieser Erklärung können wir die eingangs angeführten Beispielbretter präzise beziffern. Hier noch einmal Abbidung FIXME, aber dieses Mal mit ihren Werten nach der Pack-Methode (vom Computer des Autors errechnet):
FIXME
Ein besonderer Fall ist, wenn der statische Evaluator, die Brettbewertung, ein Pack mit vier gleichen Steinen findet. Dann hat jemand gewonnen und das Brett des Wertes ist "minus gigantisch" oder "plus gigantisch" -- je nachdem, ob der Mensch ("O") oder der Computer ("X") gewonnen hat. Hier braucht nichts mehr addiert zu werden. Der Computer liefert einfach einen sehr positiven oder sehr negativen konstanten Wert zurück, um zu signalisieren, dass das Spiel zu Ende ist und wer gewonnen hat -- z.B. 10000, bzw. -10000. (In der Praxis ist das wegen penibel durchdachter Sonderregeln manchmal nicht ganz so einfach, aber auch das wird in FIXME besprochen.)
Mit Hilfe des vorgestellten statischen Evaluators und seiner Pack-Liste erhalten wir eine sehr feinkörnige Brettbewertung, die den tatsächlichen strategischen Wert sehr genau widerspiegelt. Das Verfahren hat auch den schönen Vorzug, dass sich die unterschiedliche Begehrtheit der verschiedenen Felder ganz natürlich ergibt. Felder in der Mitte des Bretts sind strategisch besser gelegen und bei Spielern begehrter, weil sie mehr Entfaltungsmöglichkeiten bieten als Felder an den Rändern. Die Ecken sind strategisch gesehen am armseligsten. Der Vorzug ist, dass mit addierten Pack-Werten keine extra Programmierung für diesen Effekt notwendig ist: ein Stein in der Mitte berührt in seinem Feld mehr Packs und kommt daher bei der Werte-Addition öfter dran und wird dadurch zwangsläufig mehr wert. Hier noch einmal Abbildung FIXME:
Ausgerüstet mit dem schönen statischen Evaluator werfen wir einen zweiten Blick auf den MinMax-Algorithmus, die eingangs gestreifte Suche im Baum.
Noch einmal MinMax
Jener Teil der Software, der einer bestimmten Situation am Brett einen Wert zuordnet, heißt der "statische Evaluator" (static evaluator). Wir brauchen einen besseren statischen Evaluator, der ein Gefühl dafür hat, welche Bretter näher dran sind am Sieg und daher mehr wert -- oder weniger, wenn sie näher dran sind am Sieg des Menschen. (Wie gesagt, wir betrachten die Werte aus der Perspektive des Computers.)
