Was weiß das metalab über digitaltechnik?: Unterschied zwischen den Versionen
K |
|||
| (2 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 62: | Zeile 62: | ||
=== Aufgabe 3.10.3.2 === | === Aufgabe 3.10.3.2 === | ||
| + | |||
| + | ''Die frühere Umformung war falsch. Die hier funktioniert.'' | ||
<nowiki>y = (x0 ^ x1 ^ x2 ^ x3') | <nowiki>y = (x0 ^ x1 ^ x2 ^ x3') | ||
| Zeile 71: | Zeile 73: | ||
</nowiki> | </nowiki> | ||
| − | Wir | + | Wir können nach dem Distributionsgesetz vereinfachen, wenn die einzelnen ANDS das Vorzeichen für bestimmte Variablen teilen. Z.B. erste und zweite Zeile, |
| + | die sich x0, x1 und x2 teilen, aber das letzte 'x3 bzw. x3. So entsteht | ||
| + | |||
| + | <nowiki>( x0 ^ x1 ^ x2 ^ 'x3) v ( x0 ^ x1 ^ x2 ^ x3) = | ||
| + | = (x0 ^ x1 ^ x2) ^ (x3 v 'x3) | ||
| + | </nowiki> | ||
| + | |||
| + | So entsteht die Sub-Aussage (x3 v 'x3), welche automatisch 1 ist, passend zu den Ands in der anderen Sub-Aussage, die damit zu (x0 ^ x1 ^ x2) wird und so mit dem Ergebnis identisch ist. | ||
| + | |||
| + | Diese mathematische Erscheinung des Distributivgesetzes gilt auch für andere solche Paare. | ||
| + | |||
| + | Die dritte und die vierte Zeile teilen sich 'x0 'x1 x3, aber nicht 'x2 bzw x2, so implodieren die Pärchen auf ('x0 'x1 x3). | ||
| − | Das | + | Das fünfte und sechste Pärchen implodiert in ähnlicher Weise auf (x0 'x1 x3). |
| − | + | Neue komplette Gleichung, in distributiv geschrumpfter Form. | |
| − | <nowiki> | + | <nowiki>y = ( x0 ^ x1 ^ x2) v |
| − | + | ('x0 ^ 'x1 ^ x3) v | |
| − | + | ( x0 ^ 'x1 ^ x3) | |
| − | |||
| − | |||
| − | |||
</nowiki> | </nowiki> | ||
| − | + | Hier sehen wir, dass Zeile 2 und 3 munter weiter distributiv sind, via ('x1 ^ x3). | |
| − | <nowiki> | + | Daher: |
| − | + | ||
| − | + | <nowiki>y = ( x0 ^ x1 ^ x2) v | |
| − | + | ('x1 ^ x3) | |
</nowiki> | </nowiki> | ||
| − | + | An dieser Steille kann der Distributivschmäh nichts mehr für uns tun. | |
| + | |||
| + | === Fleißaufgabe für 3.10.3.2 === | ||
| + | |||
| + | Hier ist die Aufgabe als Lisp-Funktion: | ||
<nowiki> | <nowiki> | ||
| − | (x0 | + | (defun ex-3-10-3-2 (x0 x1 x2 x3) |
| − | + | (h-or-n | |
| − | + | (h-and-n x0 x1 x2 (h-not x3)) | |
| + | (h-and-n x0 x1 x2 x3) | ||
| + | (h-and-n (h-not x0) (h-not x1) x2 x3) | ||
| + | (h-and-n (h-not x0) (h-not x1) (h-not x2) x3) | ||
| + | (h-and-n x0 (h-not x1) x2 x3) | ||
| + | (h-and-n x0 (h-not x1) (h-not x2) x3))) | ||
</nowiki> | </nowiki> | ||
| − | + | Wahrheitstabelle: (NIL T NIL T NIL NIL NIL NIL NIL T NIL T NIL NIL T T), bzw. (0 1 0 1 0 0 0 0 1 0 1 0 0 1 1), links ist 0, rechts 15. | |
| + | Hier ist die erste Vereinfachung: | ||
<nowiki> | <nowiki> | ||
| − | (x2 | + | |
| − | + | (defun ex-my-3-10-3-2-i (x0 x1 x2 x3) | |
| + | (h-or-n | ||
| + | (h-and-n x0 x1 x2) | ||
| + | (h-and-n (h-not x0) (h-not x1) x3) | ||
| + | (h-and-n x0 (h-not x1) x3))) | ||
</nowiki> | </nowiki> | ||
| − | + | Wahrheitstabelle ist gleich. Und hier das Ende: | |
| − | |||
<nowiki> | <nowiki> | ||
| − | + | (defun ex-my-3-10-3-2-ii (x0 x1 x2 x3) | |
| + | (h-or-n | ||
| + | (h-and-n x0 x1 x2) | ||
| + | (h-and-n (h-not x1) x3))) | ||
</nowiki> | </nowiki> | ||
| + | |||
| + | ... bei konstant bleibender Wahrheitstabelle. | ||
| + | |||
| + | Das Lisp-Programm befindet sich hier, simuliert komplizierte logische Funktionen mit einfach logischen Funktionen: | ||
| + | [[logi-1.lisp]] | ||
Aktuelle Version vom 14. Januar 2018, 14:10 Uhr
In der Bibliothek findet sich Klaus Frickes Digitaltechnik, 4. Auflage; ISBN 3-528-33861-X
Oder auch nicht. Weil jemand die Metalab-Bibliothek mit einer Ausleihbibliothek verwechselt hat. Das Buch ist jetzt weg.
"Es war jedenfalls noch am 11. Jänner 2018, 18:00 da. Es müsste sich im rechts-unteren Teil des oberen Kastens befinden." -- Danke, R.P. für Einscannen und Erfassen der Metalab-Bücher. Ich wusste nicht, dass diese ehrenwerte Tätigkeit gerade stattfindet. Buch habe ich inzwischen wieder in der Reissen. Befindet sich am angegebenen Ort. Sorry für Aufregung.
In der In den Büchergewölben der TU Wien erhältlich, und zwar hier: Digitaltechnik. (Ist aber die 3. Auflage.)
Spammt hier eure Lösungen für die Aufgaben hinein, sowie Fleißaufgaben. So entstehen Anlaufstellen für Spezialfragen, sowie eine Dokumentation des kollektiven Wissens.
Und so könnte der Eindruck entstehen, dass es sich beim Metalab um EXTREMSTREBER handelt. Wer Elektronik oder Software hat, die zu einer Aufgabe im Buch Digitalelektronik passt, einfach hier spammen.
Auch interessant wären Links zu populärwissenschaftlichen Aufbereitungen der einzelnen Abschnitte in Klaus Frickes Werk. Es ist nämlich ein eher schwieriges Buch und gestelztes Buch, oft unklar, mit exotischer Zeichensprache.
Hard Mode: Ohne Clifford.
Besonders für FUNKAMATEURE und ARDUINITOS geeignet! Das Werk enthält auch einen Mikroprozessorteil, der aber wegen dem 68HC11 veraltet ist. Fotos oder Videos von Mikroprozessorprojekten im Metalab könnten zeigen, dass das Metalab diese Materie völlig beherrscht. (Ja, Harald, dich mein ich, und dich, Amir!)
Endlich wieder ein kubistisches Kunstprojekt im Metalab!
Aufgabe 3.10.3.1
| x1 | x0 | v | x0 | ^ |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 |
| x1 | x0 | ^ | x0 | v |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 |
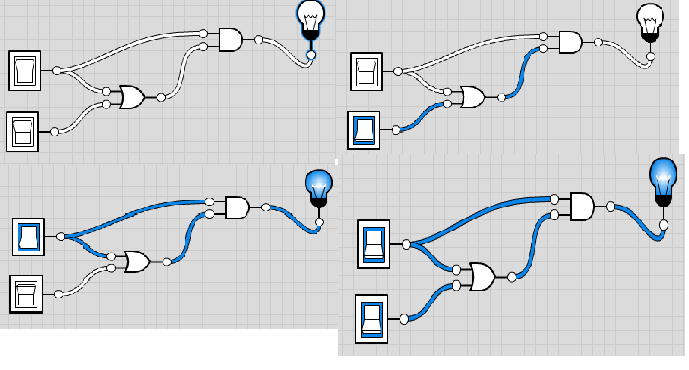
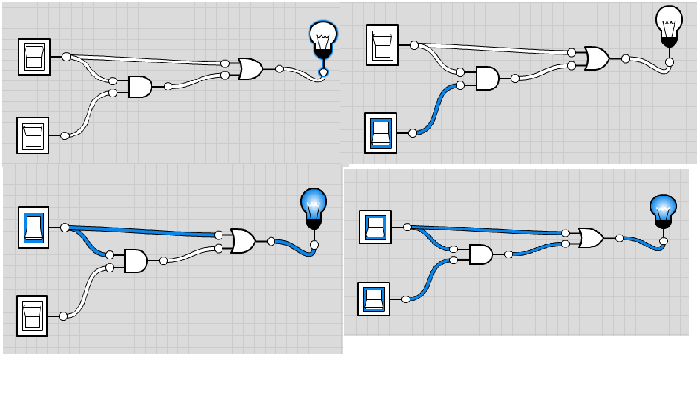
Fleißaufgabe 3.10.3.1
Hier sind die Bilder von den Logik-Simulationen, demonstrieren das Absorptionsgesetz. Der obere Schalter ist x0, der untere x1.
Der Online-Simulator ist hier: Logicly.io
Aufgabe 3.10.3.2
Die frühere Umformung war falsch. Die hier funktioniert.
y = (x0 ^ x1 ^ x2 ^ x3') v (x0 ^ x1' ^ x2 ^ x3 ) v (x0' ^ x1' ^ x2 ^ x3 ) v (x0' ^ x1' ^ x2' ^ x3 ) v (x0 ^ x1' ^ x2 ^ x3 ) v (x0 ^ x1 ^ x2 ^ x3 )
Wir können nach dem Distributionsgesetz vereinfachen, wenn die einzelnen ANDS das Vorzeichen für bestimmte Variablen teilen. Z.B. erste und zweite Zeile, die sich x0, x1 und x2 teilen, aber das letzte 'x3 bzw. x3. So entsteht
( x0 ^ x1 ^ x2 ^ 'x3) v ( x0 ^ x1 ^ x2 ^ x3) = = (x0 ^ x1 ^ x2) ^ (x3 v 'x3)
So entsteht die Sub-Aussage (x3 v 'x3), welche automatisch 1 ist, passend zu den Ands in der anderen Sub-Aussage, die damit zu (x0 ^ x1 ^ x2) wird und so mit dem Ergebnis identisch ist.
Diese mathematische Erscheinung des Distributivgesetzes gilt auch für andere solche Paare.
Die dritte und die vierte Zeile teilen sich 'x0 'x1 x3, aber nicht 'x2 bzw x2, so implodieren die Pärchen auf ('x0 'x1 x3).
Das fünfte und sechste Pärchen implodiert in ähnlicher Weise auf (x0 'x1 x3).
Neue komplette Gleichung, in distributiv geschrumpfter Form.
y = ( x0 ^ x1 ^ x2) v
('x0 ^ 'x1 ^ x3) v
( x0 ^ 'x1 ^ x3)
Hier sehen wir, dass Zeile 2 und 3 munter weiter distributiv sind, via ('x1 ^ x3).
Daher:
y = ( x0 ^ x1 ^ x2) v
('x1 ^ x3)
An dieser Steille kann der Distributivschmäh nichts mehr für uns tun.
Fleißaufgabe für 3.10.3.2
Hier ist die Aufgabe als Lisp-Funktion:
(defun ex-3-10-3-2 (x0 x1 x2 x3)
(h-or-n
(h-and-n x0 x1 x2 (h-not x3))
(h-and-n x0 x1 x2 x3)
(h-and-n (h-not x0) (h-not x1) x2 x3)
(h-and-n (h-not x0) (h-not x1) (h-not x2) x3)
(h-and-n x0 (h-not x1) x2 x3)
(h-and-n x0 (h-not x1) (h-not x2) x3)))
Wahrheitstabelle: (NIL T NIL T NIL NIL NIL NIL NIL T NIL T NIL NIL T T), bzw. (0 1 0 1 0 0 0 0 1 0 1 0 0 1 1), links ist 0, rechts 15.
Hier ist die erste Vereinfachung:
(defun ex-my-3-10-3-2-i (x0 x1 x2 x3)
(h-or-n
(h-and-n x0 x1 x2)
(h-and-n (h-not x0) (h-not x1) x3)
(h-and-n x0 (h-not x1) x3)))
Wahrheitstabelle ist gleich. Und hier das Ende:
(defun ex-my-3-10-3-2-ii (x0 x1 x2 x3)
(h-or-n
(h-and-n x0 x1 x2)
(h-and-n (h-not x1) x3)))
... bei konstant bleibender Wahrheitstabelle.
Das Lisp-Programm befindet sich hier, simuliert komplizierte logische Funktionen mit einfach logischen Funktionen: logi-1.lisp