Dome 2.0: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Ripper (Diskussion | Beiträge) FE-Simulation für den Dome + Stahlvariante |
||
| Zeile 57: | Zeile 57: | ||
=== Rohrabmessungen/Festigkeit === | === Rohrabmessungen/Festigkeit === | ||
Beim aufgebauten Dome treten verschiedene Belastungen an den Rohren auf, diese sind nachfolgend ähnlich wie auf [http://www.domerama.com/calculators/geodesic-analysis/] ermittelt. Für die Berechnung werden die | Beim aufgebauten Dome treten verschiedene Belastungen an den Rohren auf, diese sind nachfolgend ähnlich wie auf [http://www.domerama.com/calculators/geodesic-analysis/] ermittelt. Für die Berechnung werden die folgenden Rohrvarianten herangezogen: | ||
* 35x2mm Aluminium EN AW-6060 T66 | |||
* 40x2mm Aluminium EN AW-6060 T66 | |||
* 45x2,5mm Aluminium EN AW-6060 T66 | |||
* 30x2mm Stahl S355J2H | |||
Aluminium EN AW-6060 T66 weist laut [https://www.hydroextrusions.com/contentassets/2492612031044c3e88553c19ddc136da/en-aw-6060---german-rev-2-003_final_web_14-04-2016.pdf] eine Streckgrenze <math>R_{p 0,2%} \geq 160 \frac{N}{mm^{2}}</math> sowie ein E-Modul von <math>E = 69GPa = 69000 \frac{N}{mm^{2}}</math>auf.<br> | |||
Stahl S355J2H weist laut [http://www.schmolz-bickenbach.de/uploads/media/Lieferprogramm_Stahlrohre.pdf] eine Streckgrenze <math>R_{p 0,2%} \geq 355 \frac{N}{mm^{2}}</math> sowie ein E-Modul von <math>E = 210GPa = 210000 \frac{N}{mm^{2}}</math>auf. | |||
==== Biegung ==== | ==== Biegung ==== | ||
Diese Belastung tritt beim Klettern auf dem Dome auf. Die höchste Spannung tritt dabei beim längsten Rohr bei mittiger Belastung auf. Ausgehend vom Widerstandsmoment <math>W=\frac{\pi}{32}\cdot \frac{D^{4}-d^{4}}{D}</math> des Alurohrs sowie des maximalen Biegemoments <math>M_{b}=\frac{F\cdot l}{8}</math> für einen beidseitig eingespannten Stab laut [https://www.cnc-lehrgang.de/biegebeanspruchung/] ergibt sich die maximale Biegespannung <math>\sigma_b=\frac{M_{b}}{W}</math>.<br> | Diese Belastung tritt beim Klettern auf dem Dome auf. Die höchste Spannung tritt dabei beim längsten Rohr bei mittiger Belastung auf. Ausgehend vom Widerstandsmoment <math>W=\frac{\pi}{32}\cdot \frac{D^{4}-d^{4}}{D}</math> des Alurohrs sowie des maximalen Biegemoments <math>M_{b}=\frac{F\cdot l}{8}</math> für einen beidseitig eingespannten Stab laut [https://www.cnc-lehrgang.de/biegebeanspruchung/] ergibt sich die maximale Biegespannung <math>\sigma_b=\frac{M_{b}}{W}</math>.<br> | ||
Für die Berechnung wird eine Last von <math>m=150kg\rightarrow F=981N</math> angenommen, da diese auch bei der Auslegung von Leitern üblich ist. | |||
==== Zug- und Druckbelastung ==== | ==== Zug- und Druckbelastung ==== | ||
| Zeile 72: | Zeile 78: | ||
==== ToDo ==== | ==== ToDo ==== | ||
* Verbinder | * Verbinder | ||
* Scherung der Schraube | |||
* Zug- und Druckkräfte in den Rohren infolge des Eigengewichts (FEA-Tool?) | * Zug- und Druckkräfte in den Rohren infolge des Eigengewichts (FEA-Tool?) | ||
* Zug- und Druckkräfte durch Plane | * Zug- und Druckkräfte durch Plane | ||
| Zeile 108: | Zeile 115: | ||
|- | |- | ||
| Knickung <math>F_{k}</math> ||align="center"| <math>52,3 kN</math> ||align="center"| <math>96,4 kN</math> | | Knickung <math>F_{k}</math> ||align="center"| <math>52,3 kN</math> ||align="center"| <math>96,4 kN</math> | ||
|- | |||
|bgcolor="lightgrey"| Rohr 30 x 2mm ||bgcolor="lightgrey"| ||bgcolor="lightgrey"| | |||
|- | |||
| Biegespannungen <math>\sigma_b</math> ||align="center" bgcolor="#55FF55"| <math>? \frac{N}{mm^{2}}</math> ||align="center" bgcolor="55FF55"| <math>? \frac{N}{mm^{2}}</math> | |||
|- | |||
| Zugbelastung <math>F_{z}</math> ||align="center"| <math>? kN</math> ||align="center"| <math>? kN</math> | |||
|- | |||
| Knickung <math>F_{k}</math> ||align="center"| <math>? kN</math> ||align="center"| <math>? kN</math> | |||
|} | |} | ||
Eventuell sind die Biegespannungen für den 4V-Dome mit 40x2mm Rohr akzeptabel, da die echten Rohre eine kürzere freie Länge haben. | Eventuell sind die Biegespannungen für den 4V-Dome mit 40x2mm Rohr akzeptabel, da die echten Rohre eine kürzere freie Länge haben. | ||
==== FE-Analyse ==== | |||
[[Datei:Dome_2.0_halb.png|200px|thumb|right|Halb aufgebauter Dome für die Simulation]]Aufgrund der bisherigen Ergebnisse wird die FE-Analyse mittels [http://www.lisa-fet.com LISA FEA] (Bei Verwendung und insbesondere Vergabe der Einheiten das [http://www.lisafea.com/pdf/manual.pdf Manual] beachten!) nur für die Domeform 4V 1/2 in den Rohrvarianten Aluminium 45x2,5mm und Stahl 30x2mm durchgeführt. | |||
Es werden die auftretenden Zug- und Druckkräfte (Tensile Force - Element values) sowie Verformung (Displacement Magnitude) wie folgt betrachtet: | |||
{| class="wikitable" | |||
!width="200"| Domeform !!width="200"| Aluminium 45x2,5mm !!width="200"| Stahl 30x2mm | |||
|- | |||
| Voll aufgebauter Dome ||align="center"| Link hier ||align="center"| Und hier! | |||
|- | |||
|bgcolor="lightgrey"| Eigengewicht ||bgcolor="lightgrey"| ||bgcolor="lightgrey"| | |||
|- | |||
| max. Zugkraft ||align="center"| 0,127 kN ||align="center"| 0,200 kN | |||
|- | |||
| max. Druckkraft ||align="center"| 0,202 kN ||align="center"| 0,322 kN | |||
|- | |||
| max. Verformung ||align="center"| 0,09 mm ||align="center"| 0,10 mm | |||
|- | |||
|bgcolor="lightgrey"| 3 Personen + mittige Last ||bgcolor="lightgrey"| ||bgcolor="lightgrey"| | |||
|- | |||
| max. Zugkraft ||align="center"| 0,839 kN ||align="center"| 0,945 kN | |||
|- | |||
| max. Druckkraft ||align="center"| 1,446 kN ||align="center"| 1,574 kN | |||
|- | |||
| max. Verformung ||align="center"| 0,96 mm ||align="center"| 0,66 mm | |||
|- | |||
|bgcolor="lightgrey"| Windlast <math>20 kN</math> ||bgcolor="lightgrey"| ||bgcolor="lightgrey"| | |||
|- | |||
| max. Zugkraft ||align="center"| 2,427 kN ||align="center"| 2,668 kN | |||
|- | |||
| max. Druckkraft ||align="center"| 2,430 kN ||align="center"| 2,647 kN | |||
|- | |||
| max. Verformung ||align="center"| 2,3 mm ||align="center"| 2,2 mm | |||
|- | |||
| Halb aufgebauter Dome ||align="center"| Link hier ||align="center"| Und hier! | |||
|- | |||
|bgcolor="lightgrey"| Eigengewicht ||bgcolor="lightgrey"| ||bgcolor="lightgrey"| | |||
|- | |||
| max. Zugkraft ||align="center"| 0,063 kN ||align="center"| 0,101 kN | |||
|- | |||
| max. Druckkraft ||align="center"| 0,064 kN ||align="center"| 0,096 kN | |||
|- | |||
| max. Verformung ||align="center"| 0,8 mm ||align="center"| 1,8 mm | |||
|- | |||
|bgcolor="lightgrey"| 3 Personen ||bgcolor="lightgrey"| ||bgcolor="lightgrey"| | |||
|- | |||
| max. Zugkraft ||align="center"| 0,709 kN ||align="center"| 0,901 kN | |||
|- | |||
| max. Druckkraft ||align="center"| 1,020 kN ||align="center"| 1,441 kN | |||
|- | |||
| max. Verformung ||align="center"| 3,2 mm ||align="center"| 4,1 mm | |||
|} | |||
=== Verbinder === | === Verbinder === | ||
Version vom 14. März 2018, 21:06 Uhr
| Language: | English |
|---|
| Dome 2.0 | |
| |
| Gestartet: | 27.02.2018 |
| Involvierte: | ripper, Eisbaer |
| Status: | in progress |
| Beschreibung: | like PVCdome but made from metal |
| Shutdownprozedur: | |
| Zuletzt aktualisiert: | 2018-03-14 |
Metalab Dome 2.0
Eine neuer, besserer(TM) Dome für das Metalab, als Ersatz für den PVCdome.
Zu klären sind:
- Material (Aluminium vs. Stahl)
- Größe
- Art der Eckverbinder
- Planen für Outdoor-Einsatz
- etc.
Abmessungen
Domegröße
Verschiedene Daten, Rohrlängen und Anzahl für einen Dome mit 4,5m Radius in unterschiedlichen Frequenzen:
| Domeform | 3V 5/9 | 4V 1/2 |
|---|---|---|
| Domehöhe | 5,344m | 4,5m |
| Bodenfläche | 59,588m2 | 62,577m2 |
| Rohranzahl x Länge | 30 x 1,484m | 30 x 1,139m |
| 35 x 1,720m | 30 x 1,329m | |
| 80 x 1,897m | 60 x 1,325m | |
| 20 x 1,985m | 70 x 1,408m | |
| - | 30 x 1,462m | |
| - | 30 x 1,344m | |
| Gesamtanzahl | 165 Stk. | 250 Stk. |
| Gesamtlänge | 296m | 336m |
| Gewicht bei Alurohr 35x2mm | 182kg | 207kg |
| Gewicht bei Alurohr 40x2mm | 204kg | 233kg |
| Gewicht bei Alurohr 45x2,5mm | 266kg | 302kg |
| Gewicht bei Stahlrohr 20x2mm | 411kg | 467kg |
Daten von 3V 5/9 Rechner und 4V 1/2 Rechner.
Berechnung als .ods: Datei:Dome Maße und gewichte.ods
Rohrabmessungen/Festigkeit
Beim aufgebauten Dome treten verschiedene Belastungen an den Rohren auf, diese sind nachfolgend ähnlich wie auf [1] ermittelt. Für die Berechnung werden die folgenden Rohrvarianten herangezogen:
- 35x2mm Aluminium EN AW-6060 T66
- 40x2mm Aluminium EN AW-6060 T66
- 45x2,5mm Aluminium EN AW-6060 T66
- 30x2mm Stahl S355J2H
Aluminium EN AW-6060 T66 weist laut [2] eine Streckgrenze sowie ein E-Modul von auf.
Stahl S355J2H weist laut [3] eine Streckgrenze sowie ein E-Modul von auf.
Biegung
Diese Belastung tritt beim Klettern auf dem Dome auf. Die höchste Spannung tritt dabei beim längsten Rohr bei mittiger Belastung auf. Ausgehend vom Widerstandsmoment des Alurohrs sowie des maximalen Biegemoments für einen beidseitig eingespannten Stab laut [4] ergibt sich die maximale Biegespannung .
Für die Berechnung wird eine Last von angenommen, da diese auch bei der Auslegung von Leitern üblich ist.
Zug- und Druckbelastung
Infolge des Eigengewichts, Windlast und anderer Belastung wirken Zug- und Druckkräfte auf die Rohre. An den Schraubverbindungen tritt die größte Belastung auf. Die maximale Last ergibt sich aus den zulässigen Spannungen und der Querschnittsfläche an der Schraubverbindung, welche der Einfachheit halber als 2 Rechtecke mit der Fläche angenommen wird zu
Annahme: M8-Schraube
Knickung
Wird das Rohr durch das Eigengewicht und andere Lasten auf Druck belastet, so ist auch die Knickung zu berücksichtigen. Entsprechend Belastungsfall 4 laut [5] beträgt die maximale Last mit sowie .
ToDo
- Verbinder
- Scherung der Schraube
- Zug- und Druckkräfte in den Rohren infolge des Eigengewichts (FEA-Tool?)
- Zug- und Druckkräfte durch Plane
- Zug- und Druckkräfte durch Wind
Übersicht aller Belastungsfälle
Die maximalen Belastungen für alle Lastfälle für die beiden Dome-Varianten:
VORSICHT: In der Festigkeitslehre wird üblicherweise ein Sicherheitsfaktor von 2 verwendet!
| Domeform | 3V 5/9 | 4V 1/2 |
|---|---|---|
| Längstes Rohr | 1,985m | 1,462m |
| Rohr 35 x 2mm | ||
| Biegespannungen | ||
| Zugbelastung | ||
| Knickung | ||
| Rohr 40 x 2mm | ||
| Biegespannungen | ||
| Zugbelastung | ||
| Knickung | ||
| Rohr 45 x 2,5mm | ||
| Biegespannungen | ||
| Zugbelastung | ||
| Knickung | ||
| Rohr 30 x 2mm | ||
| Biegespannungen | ||
| Zugbelastung | ||
| Knickung |
Eventuell sind die Biegespannungen für den 4V-Dome mit 40x2mm Rohr akzeptabel, da die echten Rohre eine kürzere freie Länge haben.
FE-Analyse

Aufgrund der bisherigen Ergebnisse wird die FE-Analyse mittels LISA FEA (Bei Verwendung und insbesondere Vergabe der Einheiten das Manual beachten!) nur für die Domeform 4V 1/2 in den Rohrvarianten Aluminium 45x2,5mm und Stahl 30x2mm durchgeführt.
Es werden die auftretenden Zug- und Druckkräfte (Tensile Force - Element values) sowie Verformung (Displacement Magnitude) wie folgt betrachtet:
| Domeform | Aluminium 45x2,5mm | Stahl 30x2mm |
|---|---|---|
| Voll aufgebauter Dome | Link hier | Und hier! |
| Eigengewicht | ||
| max. Zugkraft | 0,127 kN | 0,200 kN |
| max. Druckkraft | 0,202 kN | 0,322 kN |
| max. Verformung | 0,09 mm | 0,10 mm |
| 3 Personen + mittige Last | ||
| max. Zugkraft | 0,839 kN | 0,945 kN |
| max. Druckkraft | 1,446 kN | 1,574 kN |
| max. Verformung | 0,96 mm | 0,66 mm |
| Windlast | ||
| max. Zugkraft | 2,427 kN | 2,668 kN |
| max. Druckkraft | 2,430 kN | 2,647 kN |
| max. Verformung | 2,3 mm | 2,2 mm |
| Halb aufgebauter Dome | Link hier | Und hier! |
| Eigengewicht | ||
| max. Zugkraft | 0,063 kN | 0,101 kN |
| max. Druckkraft | 0,064 kN | 0,096 kN |
| max. Verformung | 0,8 mm | 1,8 mm |
| 3 Personen | ||
| max. Zugkraft | 0,709 kN | 0,901 kN |
| max. Druckkraft | 1,020 kN | 1,441 kN |
| max. Verformung | 3,2 mm | 4,1 mm |
Verbinder
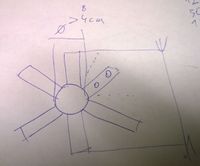
Um den Aufbau zu erleichtern sollen die Rohre einzeln mit je 2 Schrauben pro Ende an sternförmige Verbinder angeschraubt werden. Diese können aus zB 5mm Aluminium auf der CNC-Fräse zugefräst und anschließend in Form gebogen werden.
Benötigt werden folgende Verbinder:
- 65 Stk. 6-fach
- 6 Stk. 5-fach
- 20 Stk. 4-fach (am unteren Rand)
Material
Aluminium vs. Stahl, von der Mailingliste:
Normaler Baustahl hat bei gleicher Abmessung das 3-fache gewicht von Alu und keine bis ca. 2x höhere Festigkeit, abhängig von der Alu-Qualität.
Er rostet wie Sau, aber er biegt sich weniger, was zu mehr Last verleitet.
Alu kostet pro kg etwa das 4-fache von Stahl, daher ist es bei gleicher Abmessung etwa 30% teurer.
- Könnte bitte irgendjemand die beiden obigen Sätze in ein verständlicheres Deutsch übersetzen? Ich ahne nur, was der Schreiber gemeint haben könnte. Hobbes (Diskussion) 21:59, 8. Mär. 2018 (CET)
(Groß)Händler für Aluminium im Großraum Wien:
Händler/Hersteller für Planen und Stoffe:
- stoff4you (Online de)
- Segelmacher Weber (Wien 19)
- Mehgies (Hersteller)
- Twitchell (Hersteller, ripper hat dort beruflich mal viele Muster kostenlos bekommen)
Planungstreffen
2018-03-08
- Anfrage für die 4V 1/2 Variante in 40x2mm Alu geht an verschiedene Händler.
- Planen: 1,5 oder 3m Stoffbreite ist ideal Aufgrund der Rohrlängen, folgende Mengen wären notwendig:
- 50m x 3m
- 150m x 1,5m
- ripper hat Materialmuster von verschiedenen Herstellern, nimmt die mit.
- Eisbaer macht Zeichnungen von den Konnektoren
Anmerkungen
Rohrlängen
- Da die meisten Händler Rohrlängen von 3 bzw. 6 m anbieten, würde ich empfehlen, die Längen in etwa soweit anzupassen, daß pro Langrohr möglichst viele Abschnitte entstehen mit möglichst minimalen Restverschnitt.
Hobbes (Diskussion) 21:59, 8. Mär. 2018 (CET)
Belastungsberechnung
- Statt der Zugfestigkeit, würde ich die Streckgrenze bzw. R verwenden, da wir hier ja auch einen Sicherheitsfaktor einplanen sollten (Bei Bespannung und Montage von schwereren Sachen im Freien, dann kommen noch Winddrücke, dynamische/statische Belastungen, etc. dazu). Die Annahme von m= 100 kg erscheint mir daher für die Berechnung als zu gering.
- EN AW-6060 T6 besitzt ein R und ein R. Daraus folgt, daß in der oberen farbigen Tabelle weitere zwei grüne Felder wegfallen würden und nur noch der Wert übrigbleiben würde.
- Obige Berechnung wurde unter der Annahme getroffen, daß die Kraft mittig auf der Rohrlänge angreift. Greift die Kraft jedoch extrem nahe bei einem Knotenpunkt an, ist zu überlegen, wie dieser Knoten auszuführen ist (Montagepunkt direkt am Rohr z.b: duchgesteckte Schraube), damit es nicht zu einem Ausleiern am Rohrende kommt.
- Diverse Statikberechnungen auf dieser Seite auch ein wenig beachten [6]
Hobbes (Diskussion) 21:59, 8. Mär. 2018 (CET)
Ich find das ja auch cool
doch bei der angedachten Belastungsdimensionierung von geräumigen 9m ist halt auch darauf zu achten, dass das beträchtliche Gewicht von Stangen, Schrauben, Planen erstmal verbracht werden muss. Im Freien will man eine Bodenverankerung, die weiteres Gewicht bedeutet (ggf. auch Boden) und zB bei einer MFVIE ist ungeklärt ob uns soviel Platz zur Verfügung steht und ob die das dem Boden dort antun wollen bzw was dazwischengelegt werden muss. Für den Aufbau sind statt schlichten Leitern schon eher fahrbare Arbeitsplattformen angesagt (oder gleich eine Arbeitsbühne wie beim 10m Leih-Dome).
wir rechnen mit einem Gewicht von 230 kg für die Alu Rohre und 50-100 Kg für die Plane. eine Bodenverankerung ist nicht erforderlich. einzelne Streben wiegen nur ca.1Kg, und man kann auf
bestehenden teilen kann man klettern. Eisbaer
€2k als Budget ist toll aber in der Größe/Stabilität wirds dann schnell wieder eng.
Macht sicher ein cooles LeiwandVille Hackzelt, bei der MF wär es programmatischer Standbau aber für eine typische Stadtflucht mit effektiv eher 3 statt 4 Tagen ist es schon wieder recht viel Aufwand. Es dann gleich etwas länger rumstehen zu lassen würde bedeuten es ist dann auch unbeaufsichtigt, Passanten, Haftung bla. Lagerung im Container könnte man mit Kurt vllt arrangieren.
Lagerung sollte im Keller ohne Probleme Möglich sein, Platzbedarf ca. eine Europalette. Eisbaer
PS: Umgedreht auch für die MetaFunker als dish interessant: für EME and beyond :) --pk (Diskussion) 18:59, 14. Mär. 2018 (CET)





































